알고리즘이란 ?
-> 컴퓨터로 문제를 풀기 위한 단계적 절차
컴퓨터 프로그램은 자료구조와 알고리즘으로 구성된다고 할 수 있다.
독립적인 프로그램이 하나의 문장이라면, 자료구조는 명사이고 알고리즘은 동사인 셈 !
-
알고리즘의 특징 (Donald Knuth에 의한 정의. 1968,1973)
- 입력 조건(input) : 외부에서 제공 가능, zero or more
- 출력 조건(output) : 하나 이상의 출력을 생성해야 함, one or more
- 명확성(definiteness) : 각 명령은 모호하지 않아야 함
- 유한성(finiteness) : 유한 스텝 후 종료해야 함
- 효과성(effectiveness) : 모든 명령어들은 원칙적으로 사람에 의해 종이와 연필만으로도 수행될 수 있도록 단순하고 기본적인 것이어야 함.
"좋은 알고리즘"은 효율성(efficiency), 단순성(simplicity) 및 우아함(elegance)를 가진다.
-
알고리즘의 기술 방법
- 자연어(natural language) ; 영어, 한국어 등 - 읽기가 쉬움. 의미 전달이 모호해질 우려가 있음.
- 흐름도(flowchart) - 직관적이고 이해하기 쉬움. 복잡한 알고리즘의 경우, 그림이 상당히 복잡해짐.
- 의사 코드(pseudo-code) - 고수준 기술 방법. 알고리즘 기술시 가장 많이 사용. 알고리즘의 핵심 내용에만 집중할 수 있게 함.
- 특정 프로그래밍 언어 ; Python, C/C++, Java 등 - 정확한 기술 가능. 많은 구체적인 사항들이 알고리즘의 핵심 내용의 이해를 방해할 수 있음.
-
알고리즘의 성능 분석
- 시간 복잡도 ; 실행 시간 분석
- 실제 실행 시간을 측정 ; 알고리즘을 구현한 프로그램의 실제 실행 시간 측정.
- 알고리즘의 복잡도를 분석 ; 이론적으로 실행 시간을 예측. 주요 연산 횟수 측정. ex) T(n)
- 실제 실행 시간을 측정 ; 알고리즘을 구현한 프로그램의 실제 실행 시간 측정.
- 공간 복잡도 ; 실행시 필요한 기억공간(메모리) 분석 ex) S(n)
//실제 실행시간 측정의 예
#include <ctime>
clock_t start finish;
double duration;
start = clock();
//수행시간을 측정하고자 하는 코드
finish = clock();
duration = (double)(finish-start)/CLOCKS_PER_SEC;
//시간 복잡도 함수 계산의 예, 배열의 최대값 찾기 알고리즘 의사코드
ArrayMax(A,n)
tmp <- A[0]; //1번 대입 연산
for i<-1 to n-1 do //루프 제어 연산 제외
if tmp < A[i] //n-1번 비교 연산
tmp <- A[i]; //최대 n-1번 대입 연산
return tmp; //1번 반환 연산
//총 연산 수 = 최대 2n
-
차수 표기법
1. 빅오 표기법 (Big-O notation) : 두 개의 함수 f(n)과 g(n)이 주어졌을 때, 모든 n>=n0에 대하여 |f(n)| <= c*|g(n)|을 만족하는 2개의 상수 c와 n0가 존재하면 f(n) = O(g(n)) 또는 f(n) ∈ O(g(n)). 함수의 상한을 표시.
예시) f(n) = 2n+1, n>=5(n0) 이면 항상 2n+1<10(c)n 이므로 f(n) = O(n) 또는 f(n) ∈ O(n)
- 위의 조건에서 항상 2n+1 < 10n2이므로 f(n) ∈ O(n2)도 가능하지만 통상적으로 차수가 제일 작은 g(n)을 쓴다.
2. 빅 오메가 표기법 (Big-Ω notation) : 두 개의 함수 f(n)과 g(n)이 주어졌을 때, 모든 n>=n0에 대하여 |f(n)| >= c*|g(n)|을 만족하는 2개의 상수 c와 n0가 존재하면 f(n) = Ω(g(n)) 또는 f(n) ∈ Ω(g(n)). 함수의 하한을 표시.
예시) f(n) = 2n2+1, n>=1이면 항상 2n2+1>=n 이므로 2n2+1 ∈ Ω(n), 2n2+1 ∈ Ω(n2)
3. 빅 세타 표기법 (Big-θ notation) : 두 개의 함수 f(n)과 g(n)이 주어졌을 때, 모든 n>=n0에 대하여 c1|g(n)| <= |f(n)| <= c2*|g(n)|을 만족하는 3개의 상수 c1, c2와 n0가 존재하면 f(n) = θ(g(n)). 함수의 하한인 동시에 상한을 표시.
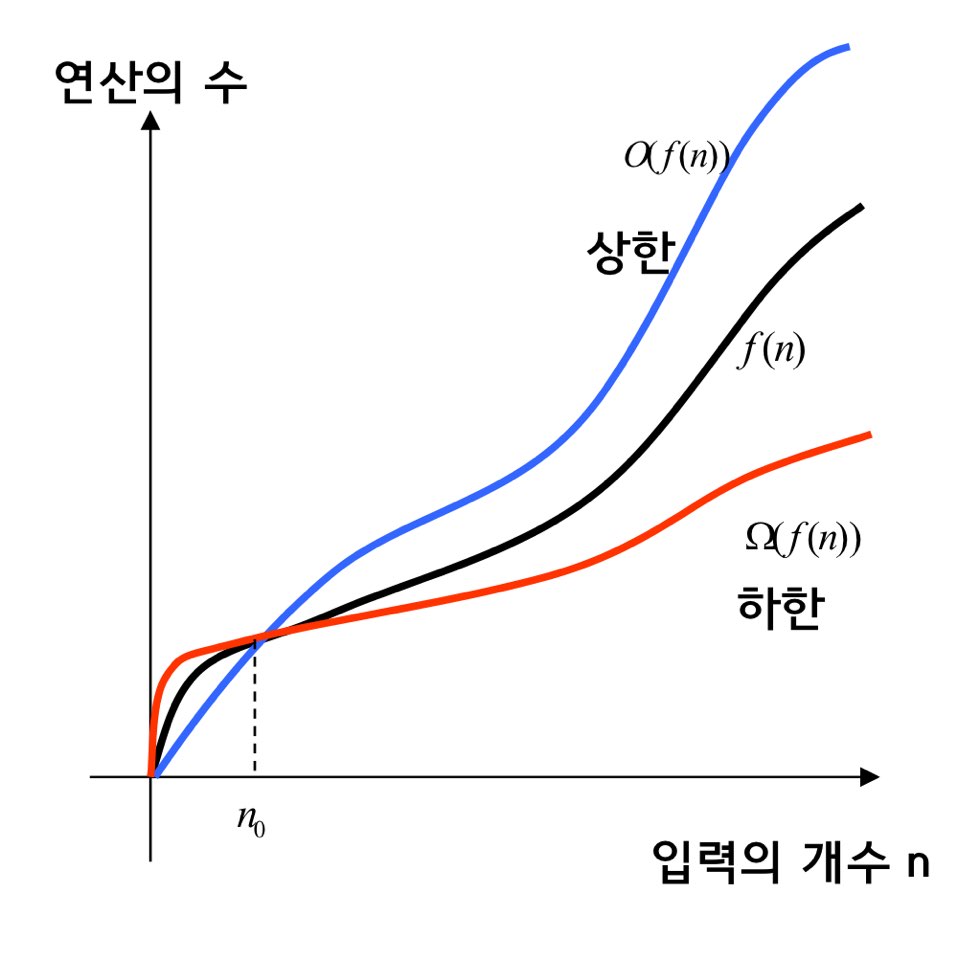
최선의 경우, 평균의 경우, 최악의 경우 중에서는 실행시간이 가장 오래 걸리는 최악의 경우(상한)를 구하는 방법이 가장 널리 사용된다. 최선의 경우는 의미가 없는 경우가 많아서 잘 쓰이지 않고, 평균의 경우는 확률적인 가정을 통해 정확히 계산하기가 어렵기 때문이다.
차수표기법을 이용하면 실행시간은 입력의 개수인 n의 함수로 나오기 때문에 입력의 크기에 따라 실행시간에 큰 차이가 날 수 있으며, 계수보다 차수가 더 큰 차이를 만들어 낸다.

또한, 2n과 n!의 시간복잡도함수를 가지는 프로그램은 압도적으로 큰 연산값이 도출되기 때문에 이 점을 유의할 필요가 있다.
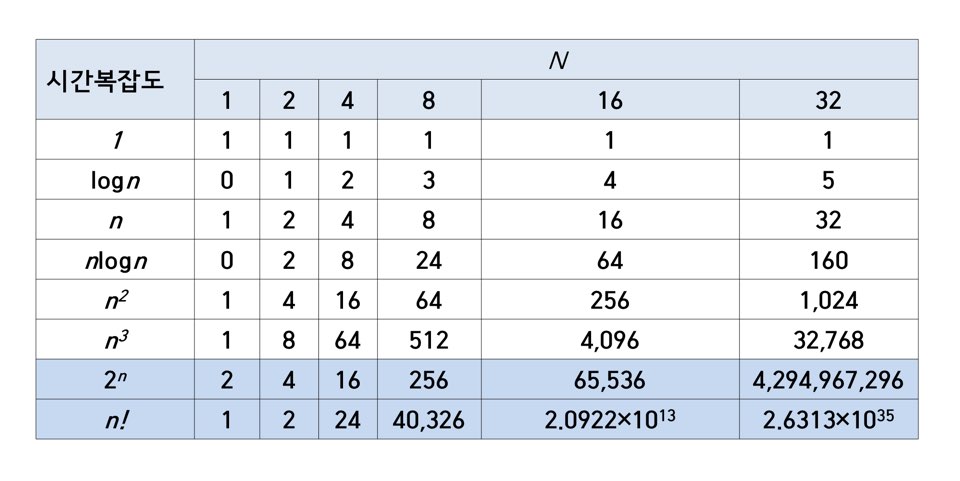
마지막으로 정리해보자면, 알고리즘이란 자료구조와 함께 프로그램을 구성하는 중요한 요소 중 하나다. 자연어, 의사코드 등으로 표현할 수 있으며 알고리즘의 성능을 분석하는 단위에는 시간복잡도와 공간복잡도가 존재한다. 차수표기법에는 빅오 표기법, 빅오메가 표기법, 빅세타 표기법이 있으며 이 중 가장 많이 사용되는 것은 빅오 표기법이다. 시간복잡도함수의 그래프와 증가양상은 알아두면 좋다.
'CS > 알고리즘' 카테고리의 다른 글
| DAG와 위상정렬(topological sort) (0) | 2021.04.06 |
|---|---|
| 최단 경로 - 다익스트라 알고리즘(Dijkstra Algorithm) (0) | 2021.04.06 |
| 최소 스패닝 트리(MST, Minimum Spanning Tree); 프림, 크루스칼 알고리즘 (0) | 2021.04.06 |
| 강한 연결 요소(SCC) ; 타잔 알고리즘과 코사라주 알고리즘 (0) | 2021.04.01 |
| 깊이우선 탐색(DFS)와 너비우선 탐색(BFS), 응용 ; 연결 성분 찾기 (0) | 2021.03.31 |